Renato Alvarez-Nodarse

ANUNCIOS IMPORTANTES.

► 05-05-2025: El lunes 1 de abril habrá una tutoría de carácter general por la tarde a las 16:00 en el aula EC1.1 (el aula habitual de clases) para aclarar cualquier duda de la asignatura.

► 11-04-2025: La segunda prueba de AF será el martes 20 de mayo a las 15:30 (el horario habitual de la clase). Para ver la estructura del examen visita el apartado de evaluación de la asignatura. La duración del examen será de 2h. Conviene estar 15 minutos antes del comienzo del examen.

Horario de clases del primer cuatrimestre: Teoría y problemas de la asignatura Diferenciación de funciones de varias variables (DFVV), grupo 3 del segundo curso del Grado en Matemáticas. Martes y jueves de 11:30 a 13:30, aula EC0.6.

Horario de clases del segundo cuatrimestre: Teoría y problemas de la asignatura Análisis funcional (AF), grupo 1 del tercer curso del grado en Matemáticas. Martes 15:30 a 17:30 y jueves 9:00 a 11:00, aula EC1.1.

El horario oficial de clases de dichos grupos se pueden consultar en la web de la Facultad de Matemáticas.

Tutorías del segundo cuatrimestre: El horario de tutorías del segundo cuatrimestre es martes 17:30 a 19:00, miércoles de 11:00 a 14:00 y jueves de 11:00 a 12:30. Previa cita por e-mail. Para quedar a una hora distinta de las anteriores contactar con el profesor (vía e-mail).

Material para las clases (curso 2024/2025)

Diferenciación de funciones de varias variables

Descripción: Asignatura obligatoria del Grado en Matemáticas. Se imparte en el 2º curso, 1º cuatrimestre.

---

Material del Curso

---

1. 📽 Pinchando AQUÍ puedes ir a la web donde se ecuentran disponibles una colección de vídeos que cubren todo el temario del curso, así como las pizarras (en PDF) de las mismas. Es recomedable descargarlos.


2. 🗐 Documentación del curso:
   
   ✏ Pinchando AQUÍ puedes consultar el programa-temario del curso.
   
   ✏ Pinchando AQUÍ tienes el resumen del curso (en PDF) (este resumen, debidamente encuadernado, se puede utilizar en todos los parciales y en las convocatorias de enero y julio (1ª y 2ª) de exámenes finales de la asignatura del presente curso).
   
   ✏ AQUÍ tienes una colección de problemas del curso.
   
   ✏ Una selección de exámenes de cursos anteriores la tienes pinchando AQUÍ.
   
   ✏ Los teoremas que hay que saber probar en las distintas pruebas y exámenes te los puedes bajar pinchando AQUÍ. Las demostraciones de dichos teoremas las tienes AQUÍ. Este material NO se puede usar en los exámenes.
   
   
3. 🖵 Las transparencias del curso están hechas a partir del resumen del mismo y están pensadas para proyectarlas con un cañón de vídeo por lo que no es necesario imprimirlas.
   1. AQUÍ tienes las transparencias de la introducción al curso.
   2. AQUÍ puedes encontrar las transparencias del tema I: Propiedades de Rⁿ.
   3. AQUÍ puedes encontrar las transparencias del tema II: Continuidad y diferenciabilidad.
   4. AQUÍ puedes encontrar las transparencias del tema III: Teorema de la función implícita.
      ➤ Pinchando AQUÍ te puedes descargar un fichero de Maxima con el ejemplo resuelto en las transparencias así como otros tres ejemplos interesantes.
   5. AQUÍ puedes encontrar las transparencias del tema IV: Extremos libres y condicionados.
      ➤ Como complemento a las transparencias del tema IV tienes los ficheros de wxmaxima con varios ejemplos (pincha AQUÍ para ver los enunciados) para el cálculo de extremos libres y de extremos condicionados.
      ➤ Si quieres una colección más completa (de cursos anteriores) de problemas de extremos condicionados la tienes aquí: enunciados en pdf y fichero de wxmaxima para extremos condicionados.
   
   
4. 🗎 Pinchando AQUÍ puedes descargate cuatro proyectos de la asignatura que puedes realizar. Dichos proyectos son voluntarios y solo ayudarán a mejorar cualitativamente la nota final de la asignatura. Cada proyecto se pueden hacer individualmente o en grupos de a lo más dos personas y ha de realizarse en su totalidad. Se pueden hacer uno o más proyectos, pero para que tengan validez hay que discutirlos con en profesor antes del examen final de la primera convocatoria de la asignatura.

1. Breve resumen de infinitésimos equivalentes
2. Resumen de las propiedades de las "o pequeñas" extraido del libro "Análisis Matemático en preguntas y problemas" de Butuzov y otros, Editorial MIR.
3. Pinchando AQUÍ puedes descargarte el libro "Introduction to Real Analysis" de William F. Trench.

A lo largo de curso usaremos el programa Maxima para resolver algunos problemas de la asignatura (especialmente en los temas III y IV). Maxima es un programa con licencia pública GNU disponible en las plataformas más usuales. Para trabajar con Maxima se recomienda el entorno de ventanas wxMaxima. Si quieres más información sobre Maxima (como descargarlo, manuales generales, etc.) visita el apartado Software Libre de Matemáticas.

➊ Con el objetivo de familiarizar al estudiante con dicho programa (que es un programa de cálculo simbólico/numérico) de forma que pueda usarlo de apoyo en el desarrollo de la asignatura, se dará una primera sesión introductoria (que se anunciará con suficiente antelación). En dicha sesión veremos una breve introducción a Maxima para, a continuación, resolver distintos problemas tipo: representación gráfica de funciones escalares de dos variables, cálculo de matrices jacobianas, derivadas parciales y direccionales, cálculo y representación gráfica de planos tangentes, etc.

Material para la sesión:
• Transparencias 1ª sesión y lista de problemas a resolver con Maxima (incluido algunos de los que se resolverán en dicha sesión).
• Código con los contenidos de la 1ª sesión en formato wxm

➋ Puedes decargarte un programa de Maxima para dibujar funciones escalares de dos variables pinchando AQUÍ.

➌ Recuerda que puedes descargarte los ficheros de Maxima para resolver problemas de funciones implícitas y de extremos libres y condicionados que se usaron en los temas III y IV (ver el apartado Transparencias del curso).

➍ Finalmente, tendremos una sesión (que será en la última semana de clases) donde trabajaremos el cambio de variables en expresiones que contengan derivadas parciales.

Material para la sesión:
• Transparencias 2ª sesión (cambio de variables).
• Código con los programas para la 2ª sesión (cambio de variables).

Si no estás familiarizado con Maxima es recomendable (aunque no imprescindible) que consultes un manual introductorio. Por ejemplo, puedes consultar las secciones 2.1, 2.3, 3.1 y 4.1 del manual del curso "Introducción al Maxima CAS con algunas aplicaciones" que te puedes bajar pinchando AQUÍ.

---

Evaluación

---

Pruebas y exámenes parciales

Para dar la posibilidad de aprobar la asignatura antes del examen final (o sin necesidad de él) se realizarán dos pruebas escritas a lo largo del curso, correspondientes a los siguientes grupos de temas:

1. Primera prueba: temas 1 y 2. Mediados de noviembre de 2024.
2. Segunda prueba: temas 3 y 4. La última semana de clases.

Estas pruebas se evaluarán sobre 10 puntos cada una. Hay que obtener al menos 4 puntos en cada prueba siendo la nota final la media de las notas de cada prueba. El resultado de las pruebas tiene carácter liberatorio respecto de la primera convocatoria de la asignatura siempre que la media de ambas supere los 5 puntos.

Los alumnos que así lo deseen pueden, en vez de realizar las pruebas anteriores, presentarse a cualquiera de las convocatorias oficiales del examen final. La máxima puntuación del examen final es de 10 puntos. Las fechas de dichos examenes finales se rigen por el calendario oficial aprobado en la Facultad de Matemáticas.

Los teoremas que hay que saber probar en las distintas pruebas y exámenes te los puedes bajar pinchando AQUÍ. Para la primera prueba son los Teoremas del 1 al 9 (T. de Taylor) y para la segunda el resto. Para los exámenes finales son todos los teoremas del 1 al 12.

✍ Se recuerda además a los alumnos que en todas las pruebas y exámenes (excepto en la 3ª convocatoria) se puede usar el resumen de la asignatura (debidamente encuadernado).

Para aprobar la asignatura hay que obtener al menos 5 puntos como nota final. Para más detalle consultar el programa de la asignatura, o directamente al profesor.

Análisis Funcional

Descripción: Asignatura optativa del Grado en Matemáticas. 2º cuatrimestre. Recomendada a estudiantes de 3º y 4º cursos del Grado en Matemáticas.

El Análisis Funcional es una de las ramas más interesantes del análisis. Resumir de lo que trata un área tan vasta es casi imposible. Una buena introducción histórica se puede consultar en este interesante artículo de Berta Gamboa de Buen o en este otro de Fernando Bombal. Un estudio histórico mucho más completo escrito por G. Birkhoff y E. Kreyszig lo puedes consultar on line o descargarlo pinchando AQUÍ.

También puedes leer el Capítulo 2 de las Notas del curso de Análisis Funcional que puedes descargar pinchando AQUI.

---

Material del Curso

---

Para ver el programa del Grupo 1 pincha AQUI

🗐 Un resumen (actualizado el 13 de marzo de 2025) del curso se puede descargar pinchando AQUI. Este resumen, grapado o encuadernado, se puede usar en las pruebas y en los exámenes finales de la 1ª y 2ª convocatorias de la asignatura. Al final de los capítulos se encuentra la lista de teoremas, resultados y problemas que hay que saber demostrar y resolver.

🕮 Las notas del curso, actualizadas a día 5 de mayo de 2025, se pueden bajar pinchando AQUI. Este material NO se puede usar en las pruebas ni exámenes.

Importante: Las notas del curso contienen todo el material del curso a expensas de las erratas que pudieran encontrarse. Si es el caso se agradecería mucho que me la hicierais llegar.

🖼 Las transparencias del curso están hechas a partir del resumen del mismo (y siguen el mismo orden del mismo) y están pensadas para proyectarlas con un cañón de vídeo por lo que no es necesario imprimirlas.

🀲   Para ver las transparencias de la primera clase pincha AQUI

🀹   Para ver las transparencias del tema "Espacios métricos" pincha AQUI

🁀   Para ver las transparencias del tema "Espacios normados" pincha AQUI

🁁   Para ver las transparencias del tema "Espacios de Hilbert" pincha AQUI

🁂   Para ver las transparencias del tema "Teoría de operadores en espacios de Hilbert" pincha AQUI

🁉   Para ver las transparencias del tema "Otros resultados fundamentales del AF" pincha AQUI

⚛   Para ver las transparencias del tema Aplicaciones del AF en el mundo real pincha AQUI (historia) y AQUI (discusión de los postulados). Las cuestiones históricas de como se gestó la teoría cuántica están tomadas del capítulo 2 del curso de Mecánica Cuántica titulado Una introduccion a la Mecánica Cuántica para "no iniciados". La segunda parte, relacionada con la axiomática y la discusión de los postulados, corresponde a las secciones 4.3 y 4.4 de dicha monografía.

---

Evaluación

---

Pruebas y exámenes parciales

Sobre las pruebas parciales de AF. Para dar la posibilidad de aprobar la asignatura antes del examen final (o sin necesidad de él) se realizarán dos pruebas escritas a lo largo del curso, correspondientes a los siguientes grupos de temas:

1. Primera prueba: temas 3, 4 y 5. Durante el mes de abril de 2025.
2. Segunda prueba: temas 6 y 7. La última semana de clases.

Estas pruebas se evaluarán sobre 10 puntos cada una. Hay que obtener al menos 4 puntos en cada prueba siendo la nota final la media de las notas de cada prueba. El resultado de las pruebas tiene carácter liberatorio respecto de la primera convocatoria de la asignatura siempre que la media de ambas supere los 5 puntos.

La lista de teoremas, resultados y problemas que hay que saber se puede encontrar al final de los capítulos 3, 4, 5, 6 y 7 del resumen del curso. Dicho resumen se puede usar el las dos pruebas y en las dos primeras convocatorias del examen.

La estructura de las pruebas será la siguiente:

• Probar uno de los teorema del apartado Teoremas principales. En la prueba habrá dos teoremas y el estudiante deberá elegir y probar uno (4 ptos).
• Probar un resultado de la selección del apartado Resultados importantes. El estudiante deberá elegir uno de los dos propuestos en el examen (3 ptos).
• Resolver dos problemas de la selección del apartado Problemas y ejercicios. El estudiante deberá elegir dos de los tres propuestos en el examen (3 ptos).

Los alumnos que así lo deseen pueden, en vez de realizar las pruebas anteriores, presentarse a cualquiera de las convocatorias oficiales del examen final. La máxima puntuación del examen final es de 10 puntos. Las fechas de dichos examenes finales se rigen por el calendario oficial aprobado en la Facultad de Matemáticas.

Sobre los exámenes finales de AF.

1. En la primera convocatoria del examen final los alumnos podrán optar por las siguientes dos opciones:
   • Recuperar cualquiera de las dos pruebas (lo que implica la renuncia a la nota obtenida en la correspondiente prueba). El esquema y condiciones de las pruebas de recuperación son los mismos que los de las pruebas originales pudiéndose usar el Resumen del curso debidamente encuadernado y sin anotaciones.
   • Realizar el examen final completo (lo que implica la renuncia a la nota por parciales). La estructura del examen final será la siguiente:
     • Probar uno de los teorema del apartado Teoremas principales. Se propondrán dos teoremas y el estudiante deberá elegir y probar uno (3 ptos).
     • Probar dos resultados de la selección del apartado Resultados importantes. El estudiante deberá elegir dos de los tres propuestos en el examen. (4 ptos).
     • Resolver tres problemas de la selección del apartado Problemas y ejercicios. El estudiante deberá elegir tres de los cuatro propuestos en el examen. (3 ptos).
     La lista completa de teoremas, resultados y problemas está al final de los capítulos 3, 4, 5, 6 y 7, del Resumen del curso. Dicho resumen se pude usar en el examen.
2. En la segunda convocatoria del examen final el alumno solo podrá realizar el examen final completo cuya estructura es la misma que para la primera convocatoria. En esta convocatoria también se puede usar el Resumen del curso.
3. En la tercera convocatoria hay que probar uno de los teorema del apartado Teoremas principales (3 ptos), dos resultados de la selección del apartado Resultados importantes (4 ptos) y resolver tres problemas de la selección del apartado Problemas y ejercicios (3 ptos). En esta convocatoria NO se puede usar el Resumen del curso.

✍ Tanto en las pruebas como en las 1ª y 2ª convocatorias oficiales se pueden usar el resumen del curso que se puede descargar pinchando AQUI. Dicho resumen no puede contener ninguna prueba ni problema resuelto. Las notas de clase NO se pueden usar en ninguna de las pruebas ni exámenes finales.

Para aprobar la asignatura hay que obtener al menos 5 puntos como nota final. Para más detalle consultar el programa de la asignatura, o directamente al profesor.

Tanto en la enseñanza como en la investigación en ciencias se hace hoy día inevitable el uso de programas de cálculo matemático (tanto programas de cáclulo numérico, como simbólico). Entre las muchas posibilidades (una lista bastante completa de las opciones se puede consultar en la wikipedia) hay que destacar los programas de software libre como, por ejemplo, Maxima y Octave, programas matemáticos con licencia GNU/GPL de cálculo simbólico y numérico, respectivamente, accesibles, gratuitos, disponibles para casi cualquier plataforma y sistema operativo y de distribución libre en internet. Conviene hacer notar que aparte de la facilidad de instalación en cualquiera de los sistemas operativos más usados (Linux, Mac, Android o Windows) de Maxima u Octave antes mencionada, también existe una gran cantidad de información en la red tales como manuales online (y en formato pdf) de los mismos.

Otra cuestión importante a la hora de decidir cuál sotware elegir es determinar si nos interesa más usar un programa numérico (en este caso la opción natural es elegir Octave) o simbólico (en cuyo caso conviene elegir Maxima.

Dado que Maxima es un programa que permite cálculos simbólicos pero también numéricos es un magnífico candidato como apoyo al estudiante y al profesor.

Para bajarte el Maxima e instalarlo en tu ordenador personal te recomendamos visites la web oficial de Maxima o bien visita la página de descargas o usa tu instalador habitual de software si usas Linux. Como entorno amigable de Maxima te recomendamos wxMaxima.

Algunos enlaces interesantes que conviene tener en cuenta son:

• Página con la documentación oficial de Maxima, incluida en su web oficial, donde además hay muchos manuales en castellano.
• Maxima tiene definida muchas funciones especiales según la notación del libro Handbook of Mathematical Functions de M. Abramowitz y I. A. Stegun (National Bureau of Standards Applied Mathematics Series - 55, 10ª Ed. 1972). Dicho manual puedes consultarlo pinchando AQUÍ o AQUÍ. También conviene revisar la NIST Digital Library of Mathematical Functions más actual pinchando AQUÍ.

Una pequeña lista de manuales interesantes es

• Breve manual escrito por Mario Rodríguez Riotorto uno de los desarrolladores de Maxima.
• Manualico para Maxima de José Manuel Mira Ros.
• Prácticas de ordenador con wxMaxima escrito por un grupo de profesores de la Universidad de Granada.
• Prácticas de Matemáticas con Maxima escrito por un grupo de profesores de la Universidad de Cádiz.

Con el objetivo de complementar los manuales existentes hemos preparado un curso introductorio de Maxima enfocado a la resolución de algunos problemas matemáticos.

El libro está dividido en ocho capítulos. En el capítulo 1 se explican los objetivos del curso y la utilidad de disponer de un programa como Maxima. El capítulo 2 constituye una brevísima introducción a Maxima incluyendo como trabajar con listas y con los principales conceptos del cálculo diferencial. En el capítulo 3 se desarrolla parte del potencial gráfico de Maxima. En el capítulo 4 se discuten algunos temas más avanzados como son la resolución de ecuaciones algebraicas, la manipulación de expresiones algebraicas, el cálculo matricial y el tratamiento de datos. Los capítulos 5, 6 y 7 se centran en el estudio de las ecuaciones diferenciales ordinarias. Finalmente, en el capítulo 8 se resuelven y proponen diversos problemas matemáticos usando Maxima.

Así que, si quieres aprender Maxima a la vez que resuelves algunos problemas de matemáticas (álgebra, cálculo, tratamiento de datos, ecuaciones diferenciales, etc.), puedes bajarte dicho texto pinchando AQUÍ. Cada sección del manual viene acompañada del correspondiente fichero de wxMaxima. Para acceder a dichos ficheros pincha AQUÍ.

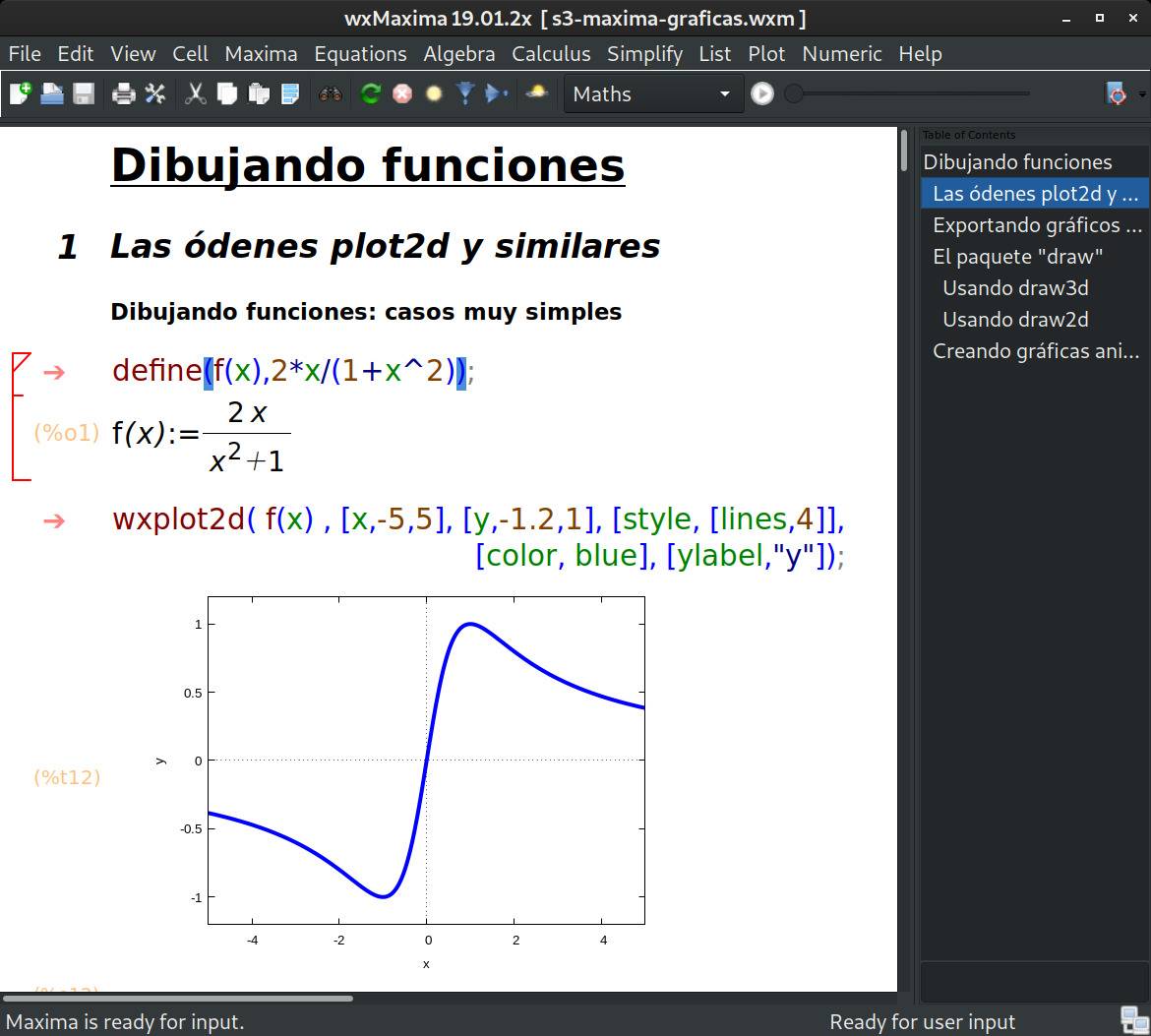Manual en PDF	Ficheros de wxmaxima

• El teorema de muestreo y sus aplicaciones, por José García Fernández. Puedes descargarte los programas pinchando AQUÍ.
• Efectos del potencial sobre la ecuación no lineal de Schrödinger, por Manuel Vera Moreno.
• Algunos aspectos matemáticos de la Teoría Cuántica de Campos, por Luis Miguel Motilla Martínez.
• Sobre la estabilidad de ciertos tipos de ecuaciones no lineales de Klein-Gordon, por Pablo Rabán Mondéjar.
• Una Teoría Unificada de las Funciones Especiales, por Enrique Martín García Martín.
• Sobre las q-series y algunas de sus aplicaciones, por Inés Balbontín Alves.
• Estudio de las soluciones de ciertas clases de ecuaciones de Schrödinger, por Guillermo Gordillo Núñez.
• Las fórmulas de Roger-Ramanujan y las funciones hipergeométricas básicas, por Regina Guerra.
• Los fundamentos matemáticos del oscilador armónico cuántico, por Juan Antonio Montalbán.
• Las funciones especiales y la teoría cuántica del momento angular, por Eva Sánchez de Toca.
• Estudio de la estabilidad de solitones en la ecuación de Schrödinger no lineal, por Fernando Carreño.

1. Si quieres ver la charla/taller titulada ¿Son las matemáticas el lenguaje de la naturaleza? que impartí el jueves 6 de marzo en la Escuela de Infórmatica (Reina Mercedes) a petición de los miembros del Club Algoritmia pincha AQUI.
2. Mis artículos de divulgación (también accesibles desde AQUÍ) en el Blog del IMUS.
3. Los números de la covid-19. En este página puedes encontrar varios artículos que hemos publicado sobre el uso de las matemáticas en temas relacionados con la pandemia de covid-19.
4. On teaching mathematics (in PDF) por V.I. Arnold (Sobre la enseñanza de las Matemáticas publicado en Russian Math. Surveys 53 (1998), No. 1, 229-236).
5. AQUÍ tienes unas frases de grandes científicos sobre la polémica "Ciencia pura o aplicada".
6. Si quieres saber que hace un profesor de Universidad pincha AQUÍ (en PDF).
7. Si quieres ver un "divertido" video sobre la educación en general y las matemáticas en particular titulado Alternative Math pincha AQUÍ.
8. Otra enlace recomendado es el magnífico video del comediante, actor y músico australiano Tim Michin titulado "Storm" que nos hace reflexionar sobre que es la Ciencia y como ha cambiado nuestra vida. En particular tiene una de las definiciones más sencillas y acertadas de ciencia (minuto 5:45) así como de lo que es la medicina (min 3:05). Para ver el corto animado subtitulado en inglés pincha AQUI. Una versión subtitulada en castellano la tienes AQUI.

Sobre Análisis

• Interactive Real Analysis (parte del proyecto MathCS).
• A Radical Approach to Real Analysis (web edition)
• Notas de Análisis Funcional de P. Garret
• Análisis Matemático en Wikipedia
• Analysis WebNotes by John Lindsay Orr (University of Nebraska-Lincoln)

Sobre EDOs

• Apuntes de EDOs por Renato Alvarez-Nodarse.
• Apuntes de EDOs por Juan Luis Varona
• EDOs en Wikipedia

El mejor libro para aprender Física jamás escrito:

• The Feynman Lectures on Physics.

Enlaces generales

• Diccionario de la Real Academia Española.
• Diccionario Oxford de Inglés
• Diccionarios de Cambrige (incluye Español-Inglés, Inglés-Español, etc.)
• Travlang's Translating Dictionaries
• The Merriam-Webster Dictionary
• Biblioteca de la Universidad de Sevilla

Libros intersantes en la red.

• Listado de libros gratis de Matemáticas.
• Encyclopedia of Mathematics.
• Abramowitz and Stegun: Handbook of Mathematical Functions On-line.
• NIST Digital Library of Mathematical Functions.
• Libros gratis de Matemáticas. Fabulosa colección de libros gratis en internet.
• Euclid's Elements The book (online)
• WWW Virtual Library for Mathematics

Historia de la Matemática, etc.

• La Exposición de libros: El legado de las matemáticas: de Euclides a Newton, los genios a traves de sus libros
• History of Mathematics: MacTutor Archive
• History of Mathematics Home Page
• The Calculus Page
• Mathematical Quotations Server
• DivulgaMat Centro virtual de divulgación de las matemáticas.
• Página personal de Antonio Pérez (Historia, problemas y pasatiempos matemáticos, etc)
• Biografías y Vidas Colección de biografías de personajes famosos históricos y actuales.

Enlaces relacionados con las Matemáticas

• Matemáticas Experimentales
• Mathematical Resources on the Web
• Frequently Asked Questions in Mathematics
• Interactive mathematics on the internet
• Internet Resource Collection (The Math Forum)
• Internet Resources for Analysis
• The Math Forum
• El Paraíso de las Matemáticas
• Rincón Matemático (Revista electrónica de matemática básica)
• EDUMAT Portal sobre educación matemática Divestadística: Portal de divulgación sobre estadística
• Statistical Data: The Data and Story Library
• A Catalog of Mathematics Resources on WWW and the Internet
• Lessons, Tutorials and Lecture Notes Mathematics Archives
• Mathematics web sites around the world (Penn State Math Department)

Buscar en Internet

• Duck duck go.
• Google
• Yahoo.

Cursos anteriores

Aquí puedes encontrar información de los cursos que he impartido en la Universidad de Sevilla en cursos anteriores (desde el 1999/2000) aunque sólo se mantiene el material del último año impartido.

Para cualquier consulta puedes contactar via e-mail a " ran(*)us.es ".

Cálculo infinitesimal

Titulación: 1º curso del Grado en Matemáticas. Asignatura anual.

Material del Curso

• Pinchando AQUÍ puedes encontrar el programa-temario del curso.
  
  

Primer cuatrimestre

(Material preparado por el Prof. Renato Álvarez)


• Pinchando AQUÍ puedes encontrar el un resumen del primer cuatrimestre del curso (en PDF).
  
  
• Pinchando AQUÍ puedes encontrar las transparencias del primer tema (números reales) y AQUÍ tienes la hoja de problemas del mismo.
  
  
• Pinchando AQUÍ puedes encontrar las transparencias del segundo tema (funciones) y AQUÍ tienes la hoja de problemas del mismo.
  
  
• Pinchando AQUÍ puedes encontrar las transparencias del tercer tema (sucesiones) y AQUÍ tienes la hoja de problemas del mismo.
  
  
• Pinchando AQUÍ puedes encontrar las transparencias de los temas cuarto y quinto (límite y continuidad de funciones) y AQUÍ tienes la hoja de problemas del mismo.
  
  
• Pinchando AQUÍ puedes encontrar las transparencias de los temas 6 y 7 (derivadas de funciones) y AQUÍ tienes la hoja de problemas.
  
  

Segundo cuatrimestre

(Material preparado por el Prof. Manuel Ordóñez)


• Pinchando AQUÍ puedes bajarte la colección de problemas para el segundo cuatrimestre.
  
  
• Pinchando AQUÍ puedes encontrar un resumen del tema 8 (cálculo de primitivas).
  
  
• Pinchando AQUÍ puedes encontrar un resumen del tema 9 (integral de Riemann).
  
  
• Pinchando AQUÍ puedes encontrar un resumen del tema 10: Aplicaciones de la integral.
  
  
• Pinchando AQUÍ puedes encontrar un resumen del tema 11: Más sobre sucesiones de números.
  
  
• Pinchando AQUÍ puedes encontrar un resumen del tema 12: Series de números.
  
  
• Pinchando AQUÍ puedes encontrar un resumen del tema 13. Los números complejos.
  
  

• Infinitésimos equivalentes
• Cálculo de derivadas
• Tabla de primitivas
• Solución del problema 3 de la hoja de problemas sobre la integral de Riemman.
  
  
• Resumen de las propiedades de las "o pequeñas" extraído del libro "Análisis Matemático en preguntas y problemas" de Butuzov y otros, Editorial MIR.
• Pinchando AQUÍ puedes consultar el libro "Interactive Real Analysis" de Bert G. Wachsmuth.

Proyectos

Aquí tienes unos proyectos relacionados con la asignatura que puedes realizar.

• Más sobre números reales.
• Algunos teoremas del cálculo diferencial.
• Escribir un programa con Maxima que implemente el método de bisección (usado en la prueba del Teorema de Bolzano) para calcular las raíces de una función continua. Implementar el método de Newton para el cálculo de las raíces de una función diferencialble. Compara la eficacia de ambos métodos con varios ejemplos.

---

Laboratorios de CI

---

La distribución de las sesiones de prácticas de CI es como sigue: 3 sesiones en el 1º cuatrimestre y 2 en el 2º.

En las dos primeras sesiones esencialmente trabajaremos con parte de las secciones 2.1, 2.3, 3.1 y 4.1 del manual del curso "Introducción al Maxima CAS con algunas aplicaciones" que te puedes bajar pinchando AQUÍ. La segunda sesión la culminaremos estudiando el método de Newton para calcular raíces de una ecuación. En la tercera sesión resolveremos problemas usando Maxima como herramienta de cálculo para resolver problemas de la asignatura. El material de dichas sesiones es el siguiente:

• Transparencias de las tres primeras sesiones.
• Código de Maxima de las sesión 1º (introducción), y de la sesión 2ª (sucesiones de recurrencia).
• Lista de problemas de la 3ª sesión (en PDF) y código de la 3ª sesión.

En la 4ta y 5ta sesiones (ya en el segundo cuatrimestre) aprenderemos algunos métodos de integración numérica y veremos distintas aplicaciones del cálculo diferencial e integral en la modelización de algunos fenómenos naturales. Aquí tienes un resumen de las prácticas. Los códigos de Maxima te los puedes bajar pinchando AQUÍ (integración) y AQUÍ (modelización).

Exámenes

Ejemplo de exámenes de años anteriores

Pinchando AQUÍ tienes las pruebas y el parcial del primer cuatrimestre del curso 2013/2014.

Pinchando AQUÍ tienes las pruebas y el parcial del primer cuatrimestre del curso 2014/2015. Pinchando AQUÍ tienes las pruebas y el parcial del segundo cuatrimestre del curso 2014/2015. AQUÍ tienes las pruebas y el parcial del primer cuatrimestre del curso 2015/2016.

Pinchando AQUÍ tienes el examen final del curso 2013/2014.

Pinchando AQUÍ tienes el examen final del curso 2014/2015.

Pinchando AQUÍ tienes los examenes finales del curso 2015/2016.

Algunos ejemplos de exámenes del primer cuatrimestre con sus soluciones (cortesía de la Prof. Mª Carmen Romero Moreno): Examen 1, Examen 2, Examen 3.

Métodos Matemáticos: Análisis Funcional (extinguida)

Titulación: Licenciado en Ciencias y Técnicas Estadísticas. Primer cuatrimestre.

Material del Curso

• Pinchando AQUÍ puedes encontrar el programa-temario del curso. Si lo prefieres bajate un resumen del mismo.
  
  
• Pinchando AQUÍ puedes bajarte un breve resumen de cálculo práctico de límites.
  
  
• Pinchando AQUÍ puedes bajarte los proyectos para casa.
  
  
• Los teoremas que hay que saber demostrar para los temas 1, 2, 3 y 4 (series espacios métricos) y las definiciones, teoremas y ejercicios que hay que saber sobre espacios normados y de Hilbert (temas 5 y 6) los puedes bajar pinchando AQUÍ.
  
  
• Algunos ejemplos de exámenes: 1er parcial, 2do parcial, Examen final.

Transparencias usadas en el curso

• Transparencias del tema Números complejos
• Transparencias del tema Series de funciones
• Transparencias del tema Espacios de Banach
• Transparencias del tema Espacios de Hilbert
• Transparencias sobre Espacios de Hilbert y Mecánica Cuántica

Nota: Todas las transparencias usadas en clase, excepto las de mecánica cuántica, están hechas a partir del resumen del curso.

Ampliación de Análisis Matemático (Introducción a las ecuaciones diferenciales) (extinguida)

Titulación: Diplomatura en Estadística. Segundo curso. Segundo cuatrimestre. Pincha aquí para ver todo el material de la asignatura Ampliación de Análisis Matemático (Ecuaciones diferenciales)

Variable Compleja y Análisis de Fourier  (extinguida)

Titulación: Licenciatura en Matemáticas. Tercer Curso. Segundo cuatrimestre.

Otro material sobre series de Fourier: También te puedes bajar un resumen sobre las aplicación de las series de Fourier para resolver EDPs y la Transformada de Fourier

Algunas funciones especiales de la física matemática (extinguida)

Titulación: Doctorado de Matemáticas.

Pinchando AQUÍ puedes encontrar el programa del curso AFEFM.

El curso se dividió en tres partes. La primera consistió en una introducción a los polinomios ortogonales (PO) con un énfasis especial en los PO clásicos. La segunda parte se centró en las apliacciones de las funciones especiales en la Mecánica Cuántica. Finalmente en la tercera parte se expuso una breve introducción a distintos problemas actuales de investigación. Unas notas parciales del curso las tienes pinchando AQUÍ. También puedes bajarte el libro Polinomios hipergemétricos y q-polinomios con mucho más detalles.

Análisis Matemático I (extinguida)

Titulación: Licenciatura en Matemáticas. Primer curso. Segundo cuatrimestre.

• Aquí tienes el programa de la Asignatura (formato PDF)
  
  
• Aquí tienes el resumen de teoría y la colección de problemas de la Asignatura (formato PDF)
  
  
• Aquí tienes un resumen de las principales propiedades de los números complejos (formato PDF)
  
  
• Aquí tienes un resumen del tema de cálculo de primitivas Cálculo de primitivas (formato PDF)
  
  
• Sobre las series de potencias ver el anexo C de los Apuntes de ecuaciones diferenciales.
  
  

Métodos Matemáticos de la Física II (extinguida)

Titulación: Licenciatura en Físicas. Segundo curso. Segundo cuatrimestre.

Pinchando AQUÍ puedes encontrar el temario de la parte de Series de Fourier y Transformada de Fourier del curso Métodos Matemáticos de la Física II

Pinchando AQUÍ puedes encontrar la hoja de problemas y los teoremas fundamentales del tema de Series y transformadas de Fourier.

También puedes obtener el material adicional en formato PDF.

• Transformada de Laplace

Elementos de Análisis Matemático (extinguida)

Titulación: Licenciatura en Matemáticas. Primer curso.

Aquí puedes encontrar un resumen de de cada tema con los teoremas más importantes, ejemplos relevantes así como la correspondiente colección de problemas.

Pinchando AQUÍ puedes encontrar información sobre el curso Elementos de Análisis Matemático, como por ejemplo, el programa de la asignatura, los problemas y los teoremas principales.

Otro material

• Algunas definiciones del tema de sucesiones formato PDF
• Propiedades de las funciones derivables formato PDF
• El polinomio de Taylor formato PDF

Site info: © 2009 Renato Álvarez-Nodarse

Contador gratuito cortesía de www.digits.net